Feel＆Think

今回からは、変形と地下水流れの相互作用を考慮した、いわゆる連成問題に陽解法を適用してみます。典型的な例は圧密現象で、地下水で飽和した地盤の表面に力を加えた際に生ずる、時間に伴う地盤の沈下です。これは、表面に加えた力によって地盤が圧縮変形することで間隙水圧が増加し、その結果表面へ向かう水の流れが発生し、水が流れ出した体積分だけ地盤がさらに圧縮変形する、といった変形と地下水流れの相互作用の結果です。

まず、支配方程式と解法の概要を説明します。詳細は、「変形と地下水流れの連成問題に関する支配方程式と陽解法」をご覧ください。

地下水流れの支配方程式は次のとおりで、これまでに何度か説明しました。

ここに、φ、ρ_w、v 、S_w、n、gはそれぞれ間隙水圧、間隙水の密度、平均流速、飽和度、地盤の空隙率、重力加速度です。また、Kbは空隙弾性定数、kは地盤の透水係数、αは飽和領域で1、不飽和領域で0となる係数です。

一方、地盤ではいわゆる有効応力則にしたがって変形が生ずるものとします。ただし、以下の説明は応力やひずみの体積成分に限ります。偏差成分は間隙水圧の影響は受けないものとします。

ここに、σ_mは平均応力（全応力）、K_dは排水条件で計測された地盤の体積弾性定数です。

式(1)と式(4)には、両方に間隙水圧とひずみの項が含まれており、これらを連立させて解く必要があります。これが連成問題と呼ばれる所以です。なお、αが0、すなわち不飽和領域では両式は独立した形となり、連成問題ではなくなります。

変形と地下水流れの連成問題では、空隙弾性定数K_bが現象を大きく左右するのですが、これは次のようにして試験結果より求めることができます。非排水、飽和条件下で等方三軸圧縮試験を行い、このときの間隙水圧が計測され、平均応力増加に対する間隙水圧の増加比率βが求められたとします。

非排水条件では水の流れが無いため、式(1)の左辺を0と置いて次式が得られます。

また、構成方程式を増分形に書けば次式となります。

式(5)を式(7)に代入すると次式となり、

式(6)と式(9)の係数を比較すると、次の関係があることがわかります。

したがって、試験によりβを求め、別途排水条件での三軸圧縮試験でK_dを求めれば、K_bを定めることができます。

支配方程式の解き方は、動的緩和法（第2回、第4回）と地下水流れの陽解法（第5回）の組み合わせです。最終的に得られる式を示すと、次のとおりです。

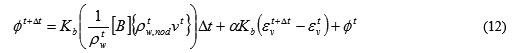
ここに、{v}は節点での間隙水の平均流速であり、節点を取り囲む要素の間隙水圧の勾配より求められます。また、[B]は勾配マトリクス、ρ_w,nodは節点での密度であり、節点を囲む要素の値を要素体積の重みを付けて平均した値とします。

なお、間隙水の密度はK_wが一定と近似して次のようにして求めることとします。

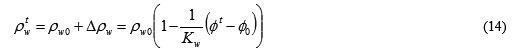
ここに、ρ_w0、φ₀は、それぞれt=0のときの間隙水の密度、間隙水圧です。

具体的な方法は、「変形と地下水流れの連成問題に関する支配方程式と陽解法」にまとめてありますのでご覧ください。式(11)と式(12)を連立させずに解くために、水の出入りを禁止するステップと、変形を禁止して水を流すステップの二つに分ける工夫をしています。

解析例として、冒頭で述べた1次元圧密問題を解いてみます。これには理論解がありますので、解析結果と比較できます。まず、水の密度変化が十分小さいことを前提に式(1)と式(3)を変形します。

また、式(4)の構成方程式を増分形に書き、1次元の全応力とひずみで書き直すと次のとおりです。なお、圧密の過程では全応力の変化はないものとします。

ここに、K_d¹は1次元圧密の場合の体積弾性定数です。
式(16)を式(15)に代入し、βを使ってK_bを消去し、

これと、

より、1次元圧密方程式が得られます。

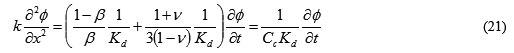
いわゆる時間係数T_vは、次のようになります。

また、圧密度Uは次のとおりです。

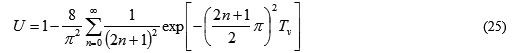
式(25)は、水が流れ始めてからの圧密度を表しますが、荷重を加えた瞬間に地盤は変形します。この瞬時変形の大きさは、次のようにして求まります。

まず、瞬時変形では水の流れが生じないため、間隙水圧変化が次のように求まります。

これを構成方程式に代入すると、次式が得られます。

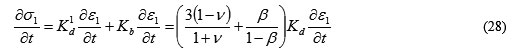
上式をもとに、加えた荷重から瞬時変形量を求めることができます。

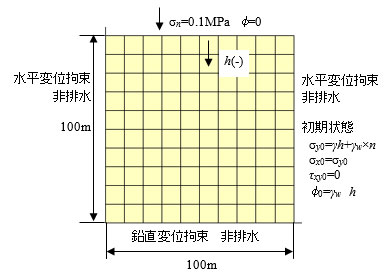
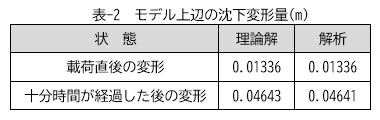
解析モデルと用いた物性値を図-1と表-1に示します。また、解析結果を動画-1と動画-2でご覧ください。まず、瞬時変形が発生し、その後地下水を排出しながら沈下変形が進行していくことがわかります。表-2に示すとおり、瞬時変形量は理論値と合致していることを確認しています。

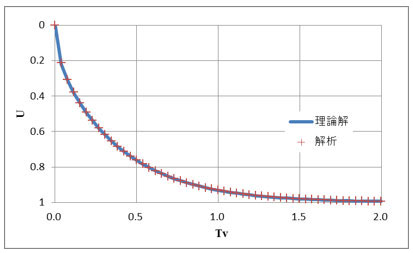
圧密過程の理論解と解析結果を比較したものを、図-2に示します。解析結果では瞬時変形からの増分を求め、圧密度を計算しています。解析結果は、理論解に一致しています。

次回は、もう少し変形と地下水流れの連成解析の例をご紹介する予定です。