Feel＆Think

今回からは、三軸圧縮試験結果を表現できる構成方程式（応力とひずみの関係を表現する理論式）を組み立ててみます。また、この理論式を用いて三軸圧縮試験をシミュレートし、実際の結果と比較します。この過程で、これまで行ってきた岩石の変形メカニズムの推定の妥当性が検証されます。さらには、岩石の挙動から地下の岩盤の挙動を想像する手掛かりを得ることができると考えます。

最初に行うのは、岩石試料に軸差応力を加えて行った際に見られた、特徴的な体積ひずみの表現です。軸差応力（圧縮応力）を加えていくと、最初は体積が減少しますが途中から膨張に転じ、有効拘束圧が大きくなると膨張が発生しにくくなることは、これまで示してきたとおりです（図-1）。

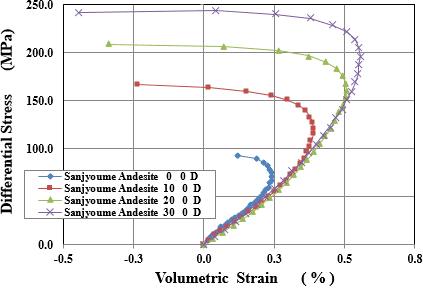
この体積膨張が、破壊した初期クラック端より発生した二次クラックの、開口を伴った伸長に起因すると考え、破壊力学をもとに二次クラックの伸長方向を検討しました。この結果、軸差応力が有効拘束圧に比べ充分に大きい場合には、開口した二次クラックは最大圧縮応力方向に伸長すると近似でき、このときの二次クラックの相対長は次式で与えられました（図-2参照）。

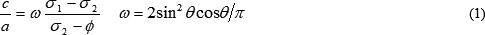
すなわち、開口した二次クラックが最大圧縮応力方向に伸長すると近似すれば、二次クラックの長さは軸差応力に比例し、有効拘束圧に反比例することになります。

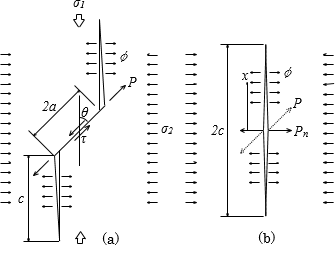
さて、最大圧縮応力方向に二次クラックが伸長する場合には、岩石の体積ひずみはどうなるのでしょうか。体積ひずみを求めるためには、二次クラックの変形から体積変化を求め、さらに二次クラックの個数分体積変化を加え合わせ、全体の体積で除すといった手続きが必要です。これを順に行っていきましょう。

まず、二次クラックの開口に伴う体積変化を求めます。図-2(b)のモデルでは、二次クラック面に作用するそれぞれの力P_n、σ₂、φによる二次クラック面の変形が、弾性論より次のように表されます。

ここに、

であり、E^*とν^*は、それぞれクラック以外の部分のヤング率とポアソン比です。ただし、これらの値は計測できません。
この変形を二次クラック面に沿って積分すれば、体積変化となります。

それぞれについて体積変化を求めると、次のようになります。

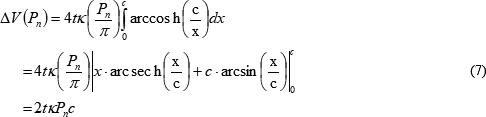
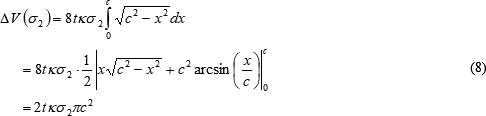
これらの和が、二次クラックがもたらす体積変化です。式(1)も考慮して、

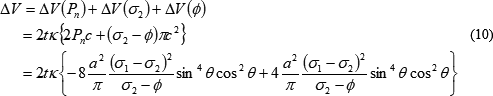
が得られます。ここで、

であり、γが初期クラックの長さaとその角度θの関数であることから、次のように書くことができます。

ここに、 であり、三軸圧縮試験では軸差応力に相当します。

二次クラックの開口による体積ひずみは、二次クラックの個数分体積変化を加え合わせ、これを全体の体積Vで除すことで求まります。

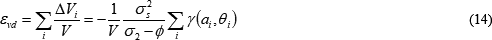
γの総和は、γの平均値 を二次クラックの個数N分加え合わせたもので近似できるものとします。

二次クラックの個数Nですが、これは破壊した初期クラックの数に他なりません。そこで、ある軸差応力で破壊する初期クラックの数を表し、全体の総和を1とする破壊密度関数Dを導入します。これに、破壊する可能性のある単位体積あたりの初期クラックの数を表すρと全体の体積を乗ずると、ある軸差応力で破壊する初期クラックの個数となります。ある軸差応力に達するまでに破壊した初期クラックの総数は、破壊密度関数をその軸差応力まで積分して求められます。

最終的に、二次クラックの開口を伴った伸長による体積ひずみは次式となります。すなわち、二次クラックによる体積ひずみは有効拘束圧に反比例します。

ここまでで、軸差応力や有効拘束圧と体積ひずみの関係は求まりました。次回は、軸差応力と軸ひずみの関係を検討しますが、軸ひずみは弾性的に挙動しているという、驚きの仮説を紹介します。