技術資料
Feel&Think
第1回 自重解析を用いた斜面の危険度評価
私たちは、数値解析を武器として、地震や豪雨になどによる地盤災害を最小化する取り組みに参加しています。数値解析では、地盤の特徴を表現できる数学モデルを用いて、降雨や地震、あるいは掘削工事などに対する地盤の応答を予測します。
解析作業では、計測結果などに基づいて数学モデルに入力する物性値を定め、適切な初期値や境界条件を与えて解析を行います。一方で、あえて極端な条件や仮想的な条件を与えて解析し、現象の特徴を引き出したり強調したりすることもできます。
本シリーズでは、このような手法により数値解析を実施し、現象の特徴を引き出したうえで、地盤の安全性を評価する新しい手法を考えます。
第1回は、斜面の危険度評価に関する試みを紹介します。
地すべりやがけ崩れに対する危険度評価には、多くの場合、地盤の傾斜といった地表面の幾何学情報が用いられます。仮に地盤の傾斜だけを危険度評価に用いた場合は、傾斜が同じであれば、斜面の高さが変わっても危険度は変わらないことになります。斜面が高くなれば法尻部に加わる荷重が大きくなり、崩壊に対する危険度は増加するはずです。幾何学情報のみを用いた評価では、斜面の応力状態が考慮されないため、このような問題が生じます。
そこで、地形を表現した3次元数値モデルを用い、自重解析を実施して応力状態を推定し、そのうえで斜面の安定性を評価してみました。地盤は弾性体で物性値は一様とし、地下水を考慮しない全応力解析を用いました。斜面の危険度評価には、地質分布や不連続面の分布、地下水の状態など様々な因子を考慮すべきですが、ここでは応力状態の影響を強調するため、あえて条件を単純化しました。
解析にはFLAC3Dを用いました。図1に地形を表現した3次元数値モデルを示します。
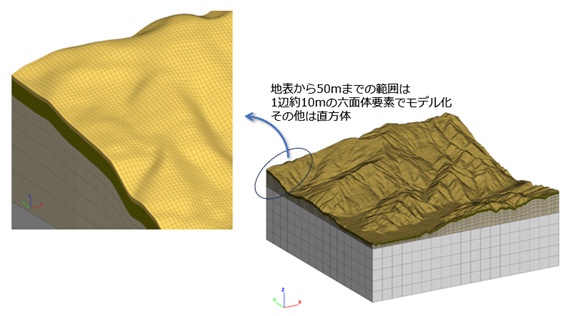
側面と下面で法線方向の変位を拘束したうえで、延長下向きに自重を加えてモデル内部の応力状態を求めました。単位体積重量は22kN/m3、ヤング率は500MPa、ポアソン比は0.3 としました。物性が一様であるためヤング率が自重による応力状態に影響を及ぼすことはありません。ポアソン比は、側面からの反力の大きさを左右するため、応力状態に影響を及ぼします。また、単位体積重量と自重による応力の大きさは比例関係にあり、単位体積重量は応力分布の傾向を変えるものではありません。
自重解析の結果をもとに斜面の危険度を表す方法を考えてみます。ここでは、各要素の応力状態と破壊条件を比較し局所安全率を定義し、この大きさで危険度を表します。
地盤や岩盤の破壊条件として最も多く用いられているのが、モールクーロン型と呼ばれるものです。安全率としては、最大せん断応力とこれに抵抗する応力の比を取ります。安全率が低いほど危険度が高くなります。
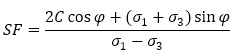
解析結果の一例を図2に示します。沢部や河川部に安全率の低い領域が見られます。斜面の危険度が高い場所は法尻部になるのが直感的です。これでは、斜面の危険度を表すものとは言えません。

これは次のような理由によるものです。
図3に、2次元の単純な斜面モデルを用い、自重解析で得られた斜面付近の主応力分布を示しました。直線の長さで主応力の大きさを、角度で主応力の方向を表しています。斜面や水平面部に沿って最大圧縮応力が分布し、法尻部に応力集中が見られます。水平面部では、斜面により押されるために水平方向の応力が大きくなりますが、垂直方向の応力は地表面付近で小さくなります。このため、水平面部の地表面付近では最大せん断応力が大きくなり、安全率が小さくなります。この結果、河川部のような水平面部で安全率が小さく評価される結果となります。
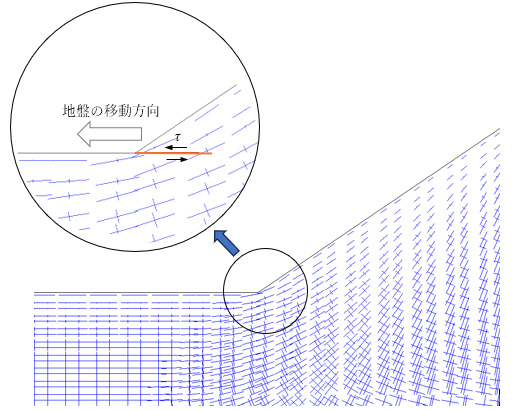
このような状態を改善するために、せん断応力として水平面内の平均せん断応力τを用いるアイデアを思いつきました。このせん断応力は、地盤が斜面を押し出そうとする方向の成分です。また、水平面部では小さい値となります。
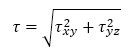
安全率は、モールクーロン型に習い、水平面のせん断応力とこれに対抗する応力の比としました。
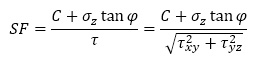
これを用いて安全率分布を描いたものが図4です。河川部などの水平に近い領域では安全率が高くなり、法尻部や急傾斜部で安全率が低くなっています。これは、直感とよく一致しています。
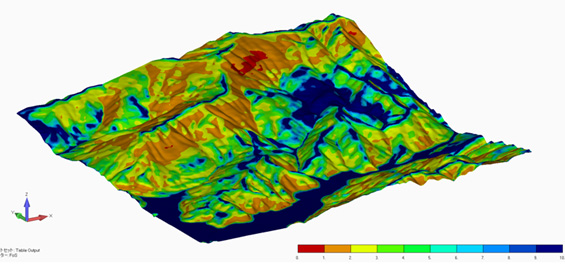
このように、数値解析を活用することによって、思いついたアイデアを具体的に表現することができました。もちろん、この評価手法の妥当性は斜面崩壊の事例と比較して検証することが必要です。ここで示した手法は一例ですが、数値解析を用いた試行錯誤を行い、より適切な評価手法にたどり着くことができると考えます。

