技術資料
Feel&Think
第7回 擬似連成解析のまとめ
前回に示した解析例では、トンネル湧水に伴う周辺地盤の変形が、完全連成解析と仮想ドレーンモデルでは大きな差異が見られました。この近似度の低さは、ここで使っている内挿関数の次数が低いことが原因です。
浸透流解析では、節点で間隙水圧を定義し、内挿関数で要素内の間隙水圧が分布していることを前提としています。ここで用いている手法は、間隙水圧の分布の近似度が低くなっているわけです。
そこで、仮想ドレーンモデルの要素を4分割し、仮想ドレーンモデルで表されるトンネル近傍の間隙水圧が分布するようにしました。仮想ドレーンモデルで求まる流量は4分割して要素に加えました。
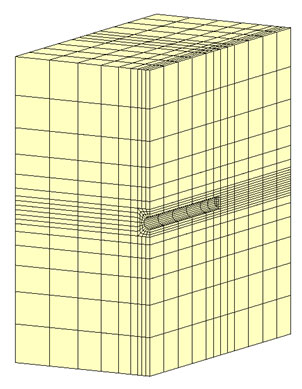
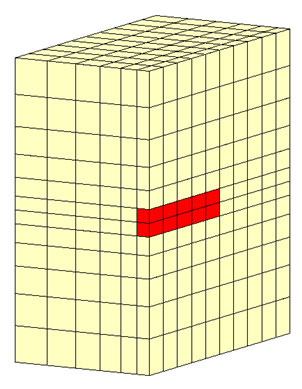
解析結果を以下に示します。
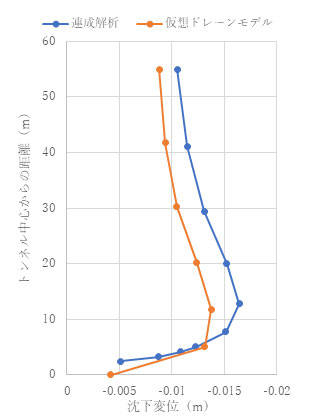
まず、鉛直方向の変位方向ですが、仮想ドレーンモデルの結果は完全連成解析の結果と良い一致が見られます。
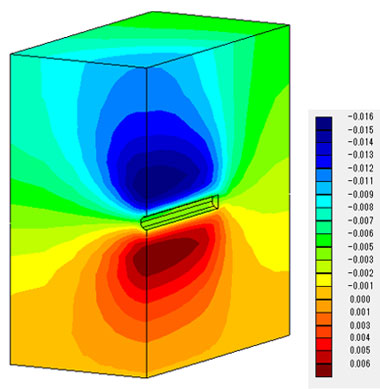
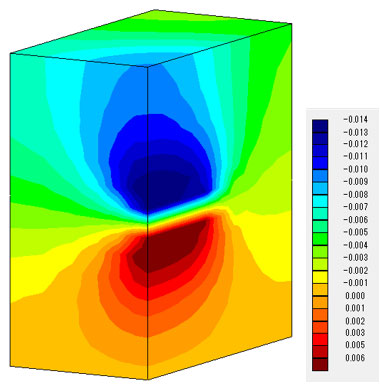
変位量を比較しても、連成解析と仮想ドレーンモデルの結果は良い一致が認められます。
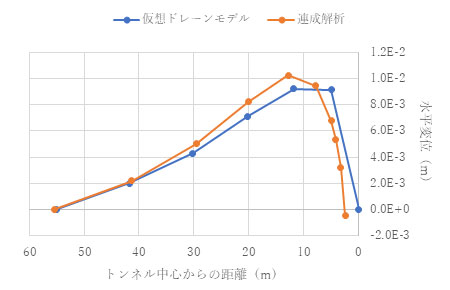
間隙水圧分布(t=1.0e+4(s))も改善され、仮想ドレーンモデルでは、あたかもトンネルが存在するかのような分布となっています。
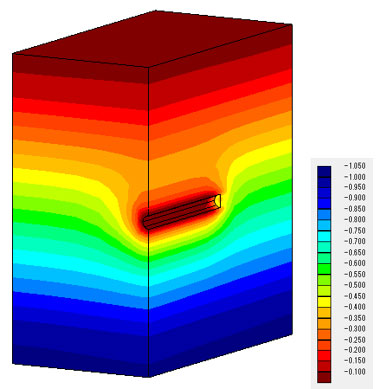
凡例の単位(MPa)
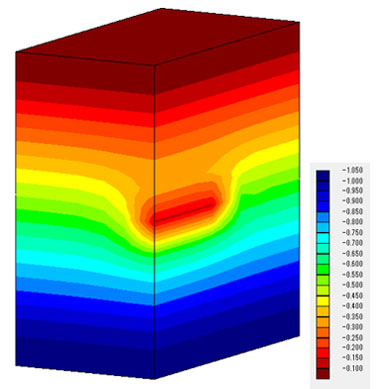
凡例の単位(MPa)
間隙水圧の値も、連成解析と仮想ドレーンモデルで良い一致が見られます。
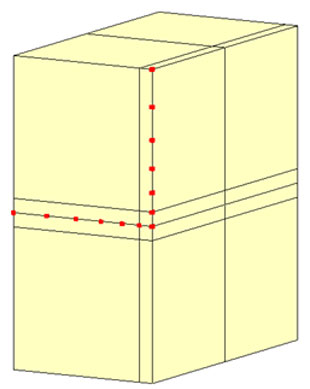
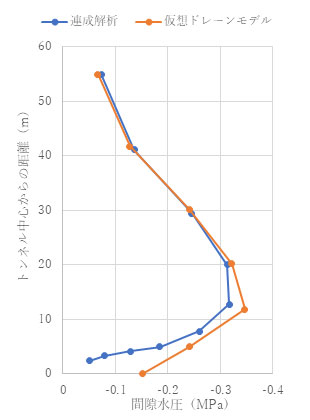
t = 1.0e+4 (s)
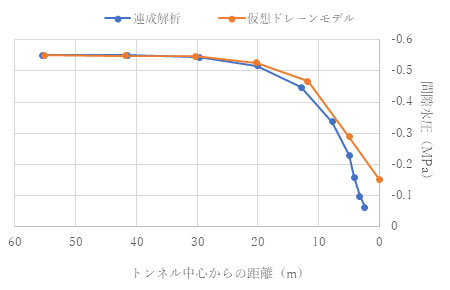
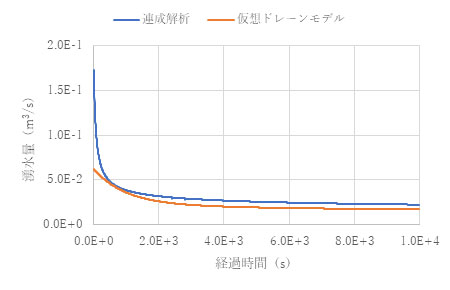
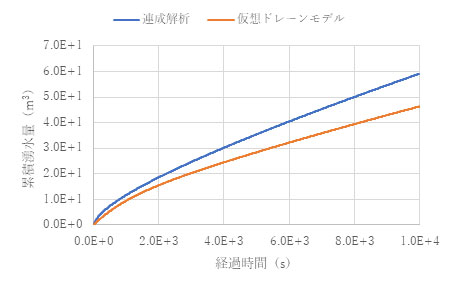
仮想ドレーンモデルの湧水量も改善しており、この結果間隙水圧分布や変位分布が連成解析に近いものとなっています。
今回のシリーズをまとめます。
トンネル掘削や地下水位低下工法などに伴う地表面沈下の予測などには、地下水流れと変形の相互作用を考慮できる連成解析が有効です。
一方で、分水界を境界とする地下水流れの解析のためには、径などに比べてはるかに広い領域が対象となります。このため、解析に用いるメッシュの節点数が大きくなることで、計算時間が長くなってしまう課題があります。もとより、変形と地下水の連成解析は自由度が大きく、時間方向にも多くの解析ステップが必要となります。
本シリーズでは、この課題を解決する方策として、次のような提案をしました。
- 地下水流れと変形を別々に解く → 疑似連成解析
- 排水構造物をメッシュ化しない → 仮想ドレーンモデル
地下水流れと変形を別々に解く疑似連成解析では、浸透流解析用ソフトで間隙水圧を求め、間隙水圧を考慮できる変形解析ソフトで変形を求めます。変形の計算はΔtごとに行う必要はなく、計算時間を短くすることができます。
一般的な境界条件では、この方法で連成解析とよく一致した解が得られます。
排水構造物をメッシュ化しない仮想ドレーンモデルでは、節点数を少なく抑えることができ、さらに計算効率が向上します。
ki-poinntoは、地下水流れの貯留係数 Ss として次式を行うことです。
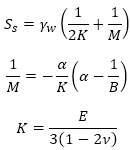
ここに、Eはヤング率、νはポアソン比、αとBは間隙弾性定数です。
仮想ドレーンモデルでは、排水構造物をメッシュ化せずに浸透流解析を行います。得られた間隙水圧を既知として変形解析を行う、擬似連成解析が可能です。
トンネル掘削の場合では、この仮想ドレーンモデルを用いた擬似連成解析が、完全連成解析を良く近似した結果となりました。なお、ここでは地下水流れの解析の改良のため、要素を分割して内挿関数の次数の低さを補いましたが、一般的な浸透流解析ソフトではこのような処理なしで計算が可能です。
仮想ドレーンモデルでは、地下水排除工のボーリングなどの存在を表現することもでき、地すべり土塊の変形を擬似連成解析で予測するなどの応用が期待できます。
是非、擬似連成解析や仮想ドレーンモデルをご活用ください。

