技術資料
Feel&Think
第6回 仮想ドレーンモデルの応用
これまで何度か述べてきましたが、連成解析の一翼を担う地下水流れの解析では、分水界を境界とする必要があるため、トンネル径や地すべり範囲に比べてはるかに広い領域が対象となります。このため、解析に用いるメッシュの節点数が大きくなることで、計算時間が長くなってしまう課題があります。
本シリーズでは、この課題を解決する方策として、排水構造物をメッシュ化しない仮想ドレーンモデルを用いる方法を提案します。3次元モデルにおいて、トンネルのような線状ドレーン構造物をメッシュ化せずに要素分割を行い、解析に要する時間を大幅に減ずる方法が仮想ドレーンモデルです。
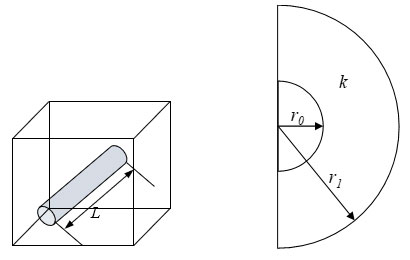
まず、トンネル直径よりも大きな辺長を持つ要素中に、仮想的にトンネルが掘削されるものとし、トンネルは円筒形で近似します。トンネル近傍では、トンネル壁面の法線方向(円筒形の径方向)に一様に地下水流れが生じているものとし、地盤の透水係数をk、径方向の座標をr、全水頭をhとして、地下水の流速uは式(1)に示すダルシー則にしたがうものとします。
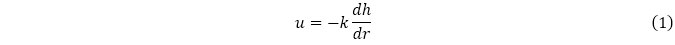
要素を横断するトンネル(円筒形)のうち、要素内部に存在する長さをL とし、この区間では長さ方向に均一に動水勾配(dh/ dr)が生じているとものとすれば、この区間のトンネル壁面からの単位時間あたりの湧水量Qeは、式(2)で与えられます。
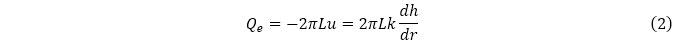
トンネルの壁面(r=r0)と壁面から離れた場所(r=r1)において、全水頭がそれぞれh0とheに保たれた場合には、 Qeは次のように求められます。
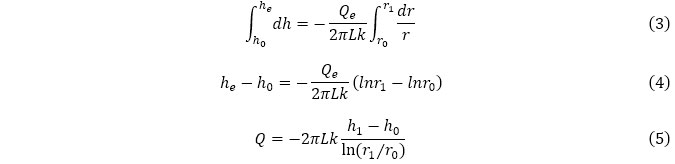
トンネルが存在する要素では、各要素構成節点で全水頭が求められますが、この節点値の平均的な値をheとすることとします。r1は、要素と同じ体積を持つ立方体に内接する球の半径とします。
排水量Qが微少時間継続した際の水頭変化を有限要素解析により求め、要素における新たな水頭値を求めます。全水頭値とトンネルのセグメント長さをもとに排水量Qの値を更新し、以下この作業を繰り返して水頭分布の変化を求めます。
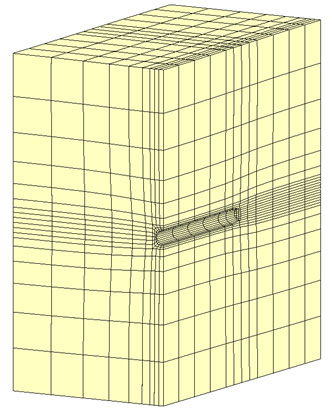
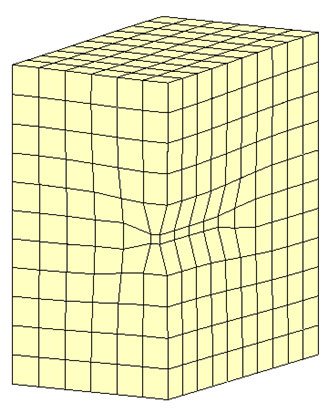
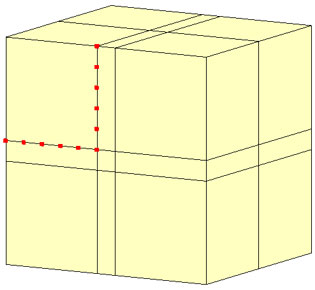
この仮想ドレーンモデルが連成解析に適用できるかどうかを、トンネル掘削問題で試してみました。完全連成解析に用いたモデルと仮想ドレーンモデルによる連成解析に用いたモデルを以下に示します。
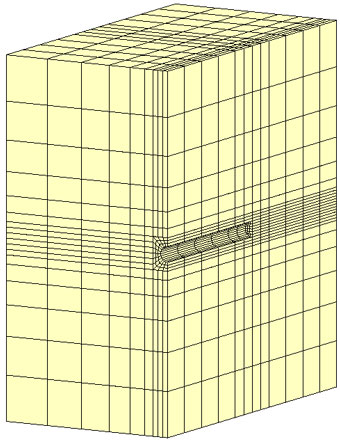
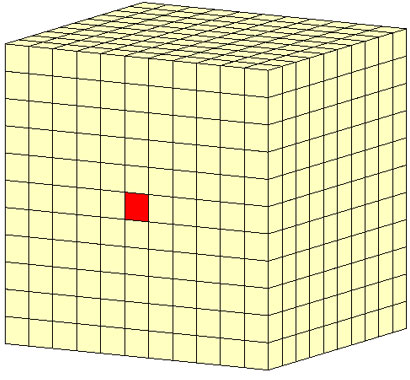
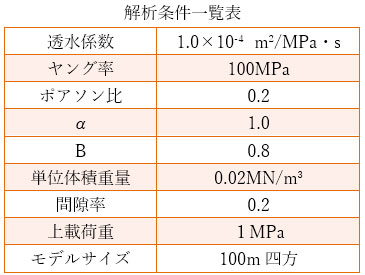
解析条件はこれまで用いたものと同じです。
完全連成解析により得られたトンネル掘削後の変形や間隙水圧変化を、仮想ドレーンモデルによる解析結果と比較します。なお、仮想ドレーンモデルでは、トンネルを含む要素の外側で断面を作成して結果を表示します。
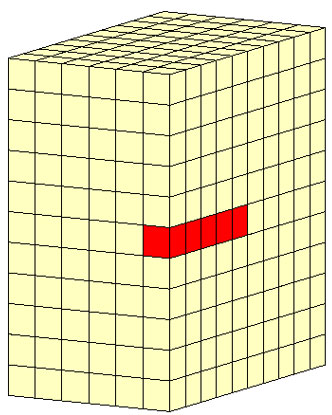
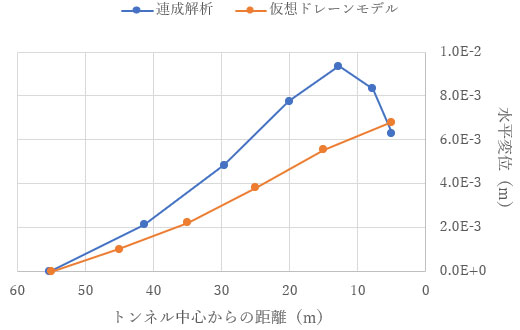
まず、t=1.0e+4(s)における変位を見てみましょう。仮想ドレーンモデルでも収縮変形が見られます。
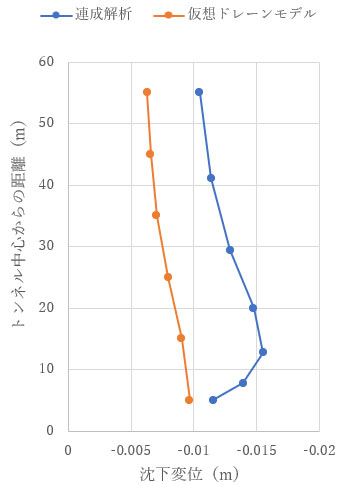
同時刻の鉛直方向の変位分布です。全体的な傾向は一致しています。
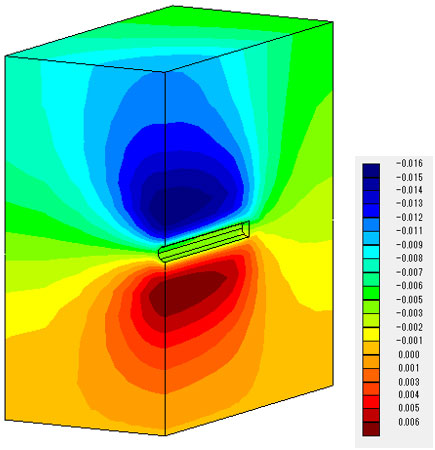
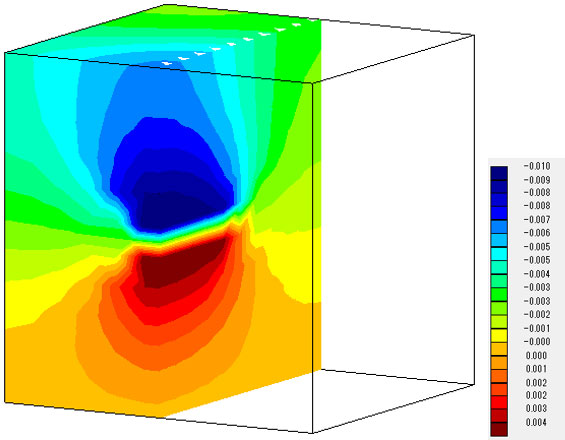
変位の値では、仮想ドレーンモデルの解は、連成解析のものに比べ変化が小さくなっています。
t=1.0e+4(s)における間隙水圧分布の比較です。傾向は似ていますが、トンネル部の間隙水圧変化が小さい値となっています。
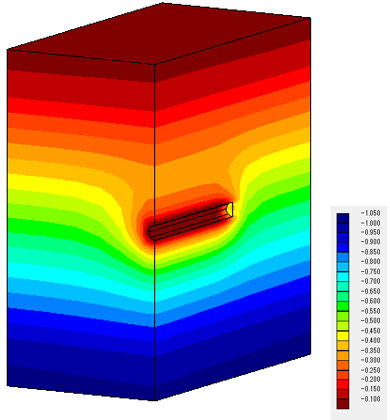
t = 1.0e+4 (s) 凡例の単位(m)
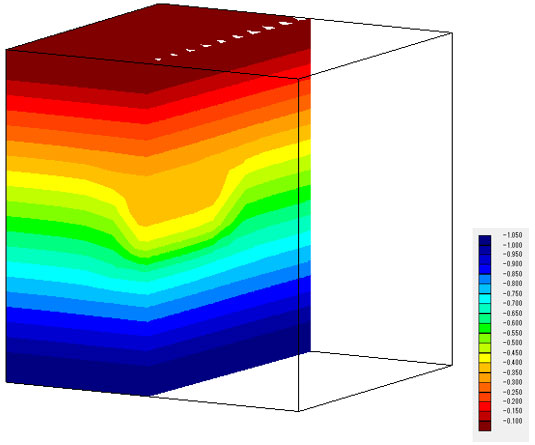
t = 1.0e+4 (s) 凡例の単位(m)
間隙水圧の値を見ても、仮想ドレーンモデルではトンネル近傍の変化が小さくなっています。
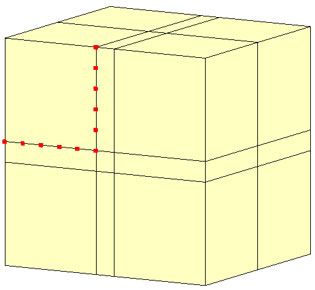
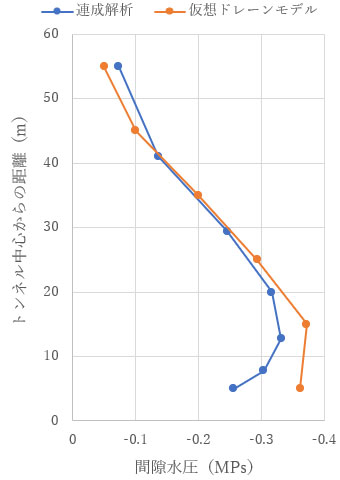
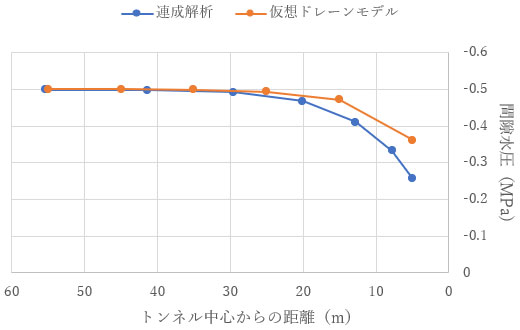
トンネルからの湧水量も、連成解析と仮想ドレーンモデルで差が見られます。
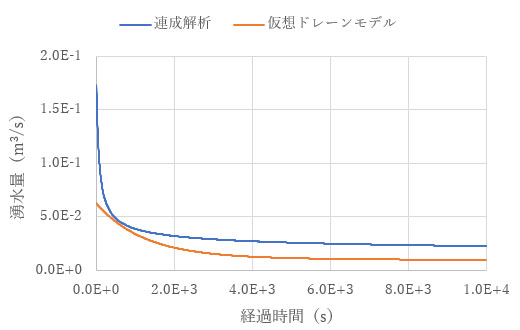
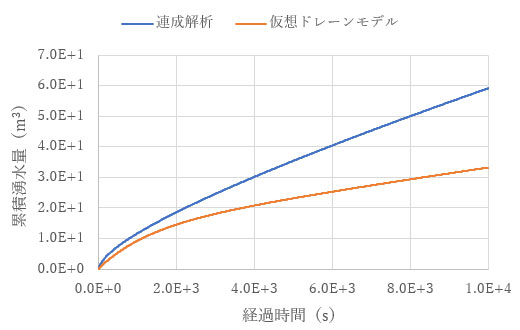
これまでの解析結果を見る限りでは、完全連成解析と仮想ドレーンモデルでは整合的ではあるものの、値に開きが見られました。次回はこの原因を探ってみます。

