Feel＆Think

これまでの例では、完全連成解析と擬似連成解析の解が良い一致を示していました。この理由の一つが、解析に用いたモデルでは、連成解析特有のMandel-Cryer効果がほとんど見られなかったためです。
Mandel-Cryer効果とは、地下水の流れに起因する間隙水圧の増減により発生した体積変形が、地下水の流れの影響がまだ達していない領域に体積ひずみを生じさせ、間隙水圧が変化する現象です。
これまで見てきた連成解析の支配方程式で説明します。

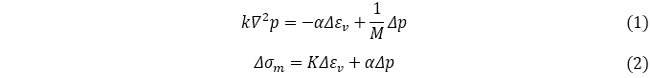
地下水の流れの影響がまだ達していない領域では次式となりますが、

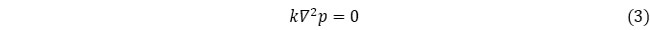
地下水流れが生じている領域では体積ひずみが発生し、これに伴う広い範囲の変形により、地下水の流れの影響がまだ達していない領域でも体積ひずみが引き起こされ、間隙水圧が発生します。

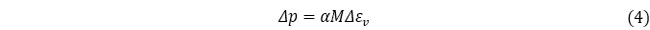
このような状態を、簡単なモデルを用い、完全連成解析により再現してみましょう。
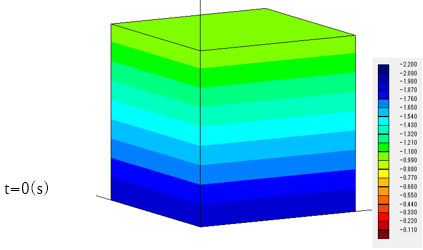
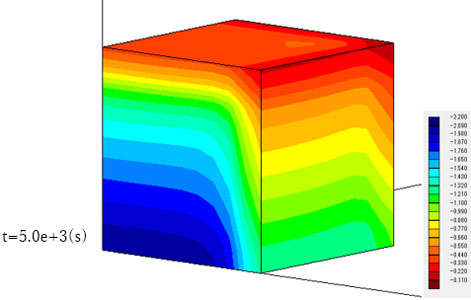
下図の立方体で、上面1MPa、下面2MPaの静水圧状態から、前方3面の水圧を瞬時に1MPa減少させた場合を想定します。後方3面は、法線方向の変形は拘束し、非排水境界とします。

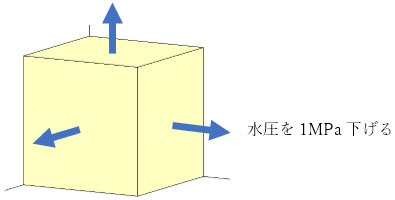
設定した条件では、前方3面から水が流出し、これにより圧縮ひずみが発生して立方体は前方から縮んでいきます。

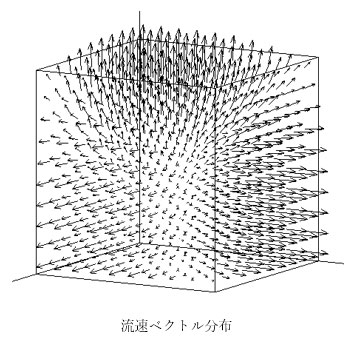
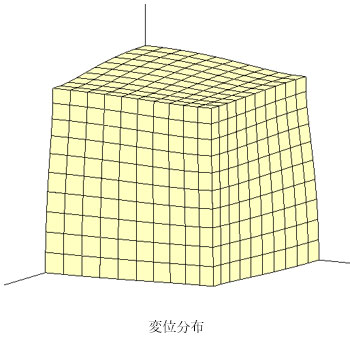
側方から見ると、前方から圧縮変形が進んでいくことがわかります。

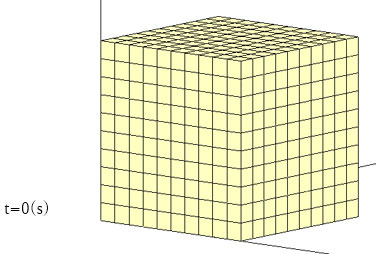
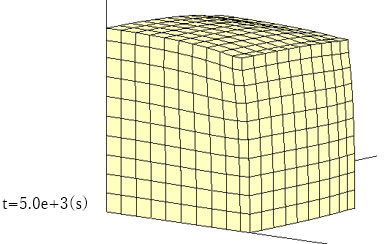
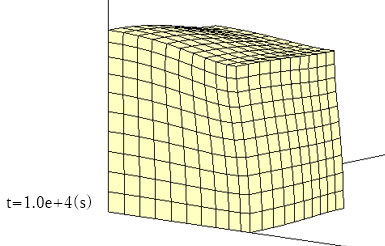
前方からでは排水が進み、間隙水圧が徐々に減少していきますが、後方は間隙水圧の減少が小さいことがわかります。

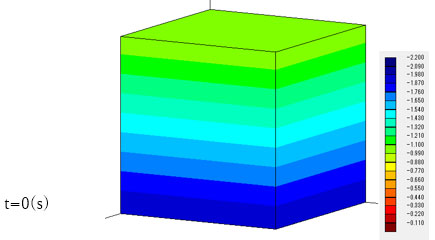
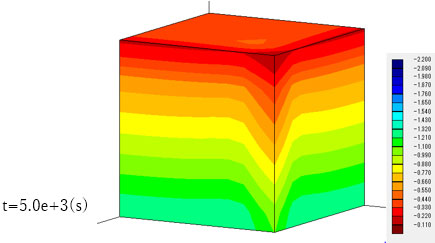
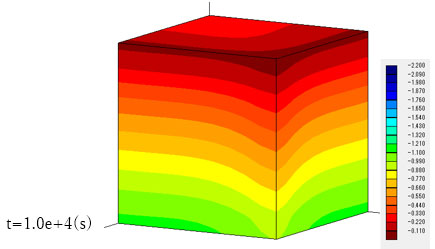
後方から見ると、モデル下部では逆に間隙水圧が増加していることがわかります。この領域では地下水流れがまだ発生していないことから、Mandel-Cryer効果による間隙水圧の上昇と考えられます。すなわち、モデル前方部で生じた地下水の流出により、モデル全体に圧縮変形が生じ、モデル奥部では地下水流れが生じていなくても間隙水圧の上昇が起こります。

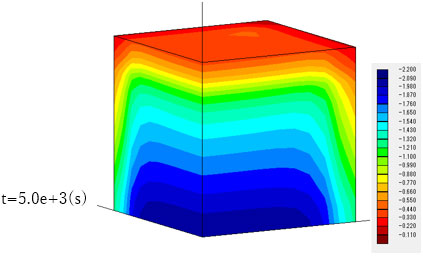
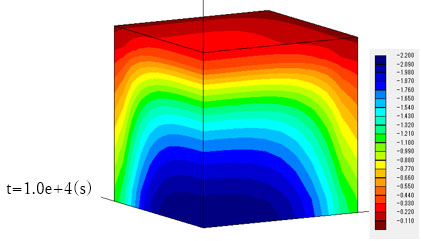
擬似連成解析の場合はどうでしょうか。擬似連成解析と完全連成解析とを比較すると、擬似連成解析ではモデル奥部における間隙水圧の増加はなく、完全連成解析ではMandel-Cryer効果により間隙水圧は増加します。

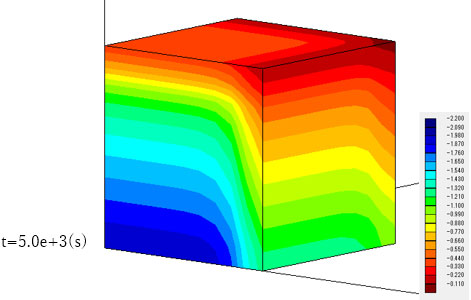
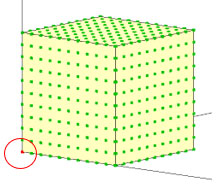
最後方部の要素の間隙水圧変化を調べると、完全連成解析では明らかに間隙水圧の増加が見られます。

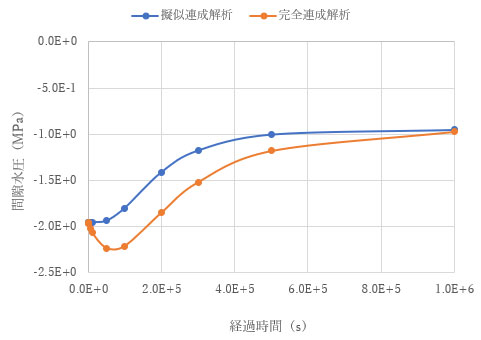
このように、Mandel-Cryer効果が発生するような境界条件では、連成解析と擬似連成解析の解は一致しません。これは、地下水流れの解析が変形を考慮せず行われているためです。
先に示した圧密の例とトンネル掘削の例では、このような条件ではないため、両方の解は一致していました。一般的な境界条件では、この例で示したような極端な条件とならず、Mandel-Cryer効果が小さいと考えられることから、擬似連成解析は良い近似を与えると考えられます。