技術資料
Feel&Think
第4回 トンネル掘削後の経時変化
前回は、圧密問題を例に擬似連成解析の実用性を検討しました。今回は、トンネル掘削の場合について考えます。
注目するのは、トンネル掘削後の変位と地下水流れの相互作用についてです。トンネル掘削後には壁面からの地下水湧出が生じ、この結果、トンネル周辺地盤では排水に伴う収縮変形が発生します。また、これにより地表面沈下も引き起こされます。
このような場合に、擬似連成解析により完全連成解析を近似した解を得ることができるかを検証します。
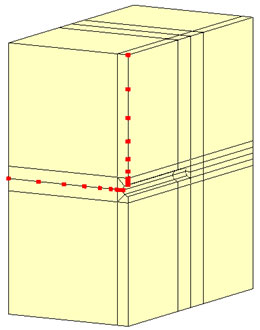
解析に用いたモデルを下図に示します。トンネルの直径は5mで、土被り55m、トンネル壁面から側方境界・底面境界まで55mとします。また、側面と底面では法線方向の変位を固定するとともに、非排水境界とします。モデル上面は間隙水圧0の境界とします。
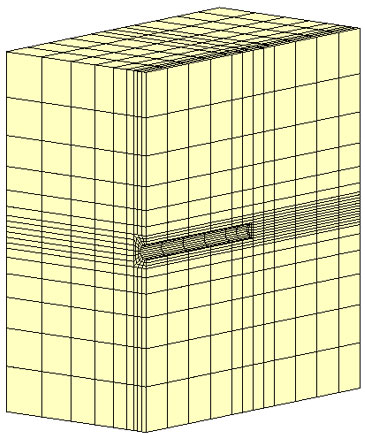
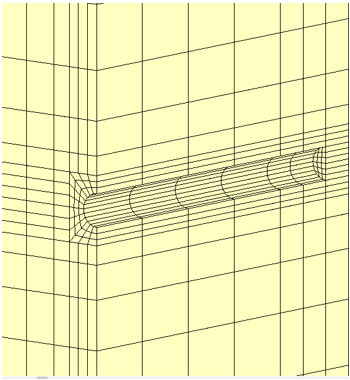
用いた解析条件を下表に一覧します。
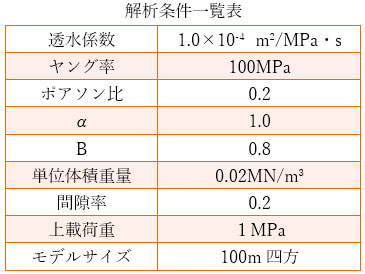
これまでと同様に、以下の3ケースで解を比較しました。

解析結果を見ていきましょう。トンネル掘削後は、トンネル内方に向かう地下水流れが生じます。
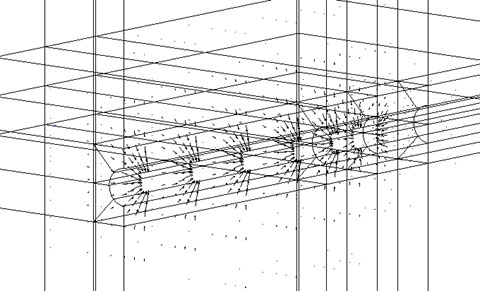
この地下水流れが地盤変形に及ぼす影響を見るため、トンネル掘削後の増分変形に注目します。増分変形は、トンネル周辺の地盤が収縮していく形になります。内空変位はほとんど発生しない点が特徴的です。
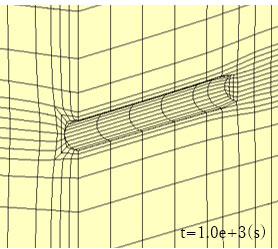
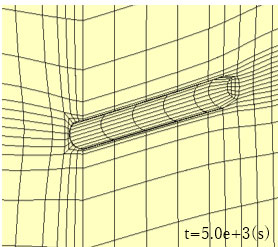
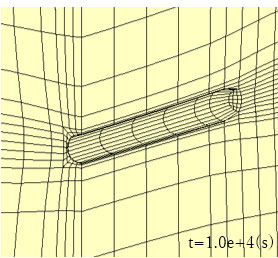
(ケース1)
解析結果を以下に示します。この解析条件ではトンネル側方の増分水平変位、上方の増分沈下変位ともに、ケース1から3でほぼ一致しています。
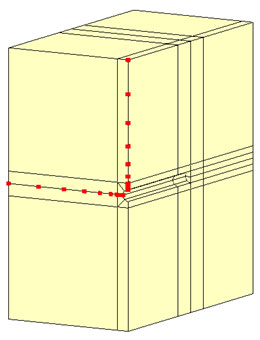
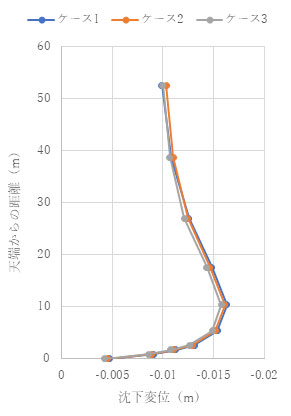
t = 1.0e+4 (s)
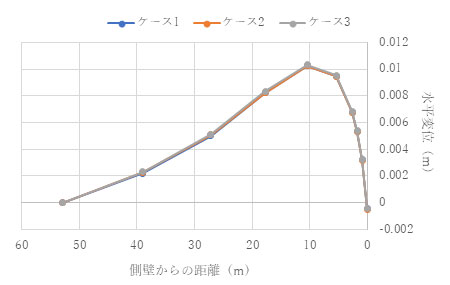
t = 1.0e+4 (s)
鉛直方向の増分変位分布を描いてみました。ケース1から3でほぼ一致していることがわかります。
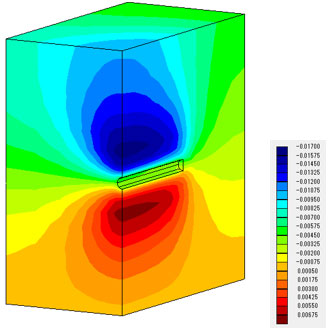
凡例の単位(m)
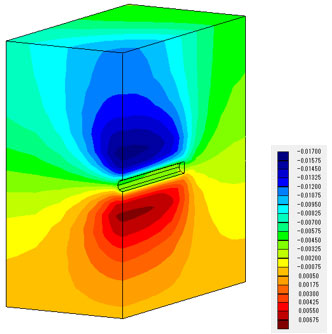
凡例の単位(m)
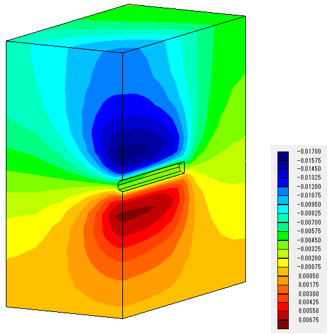
凡例の単位(m)
間隙水圧分布も調べてみました。ケース1から3でほぼ一致しています。
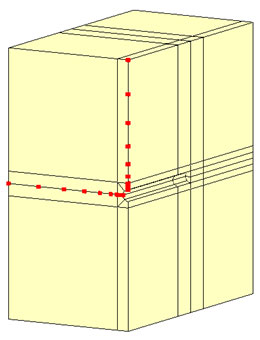
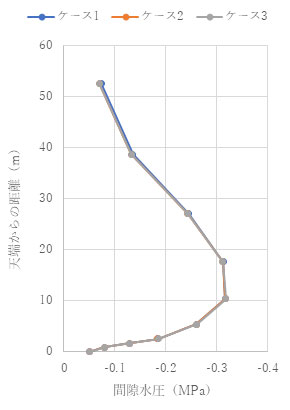
t = 1.0e+4 (s)
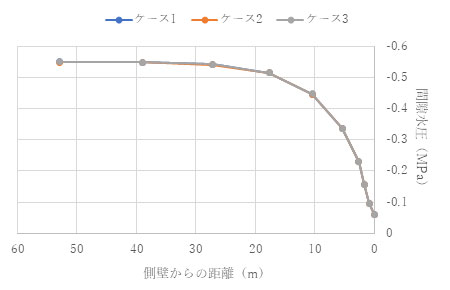
t = 1.0e+4 (s)
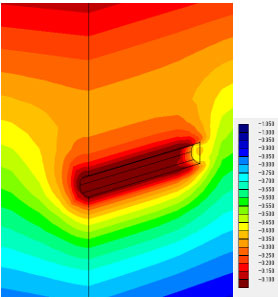
凡例の単位(MPa)
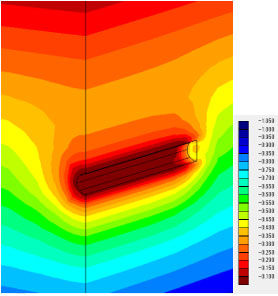
凡例の単位(MPa)
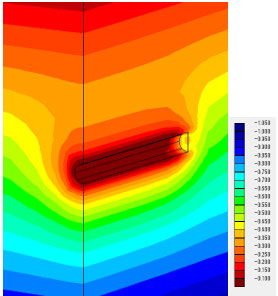
凡例の単位(MPa)
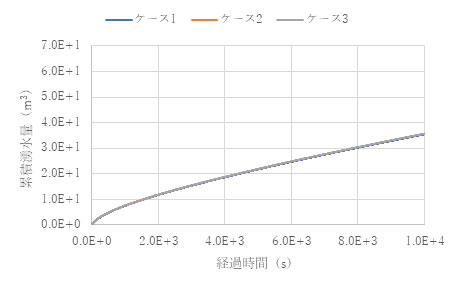
トンネル壁面からの湧水量も、各ケースで一致しています。単位時間あたりの湧水量は掘削直後で大きく、その後一定値に収束し定常状態となります。
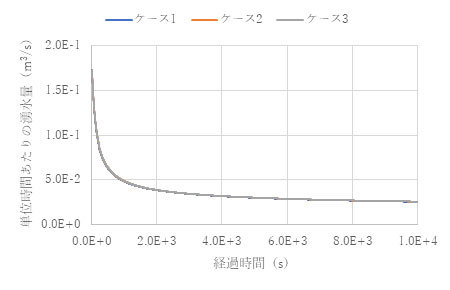
なぜこのような一致が見られるのでしょうか。第3回で示した1次元圧密方程式を振り返ってみましょう。
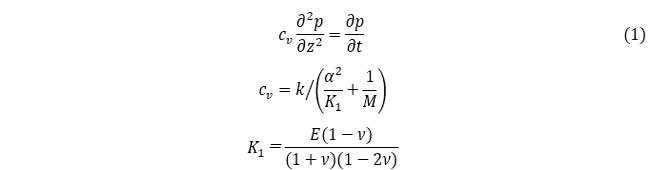
これまで使ってきた記号で記述すると、式(1)は次のようになります。
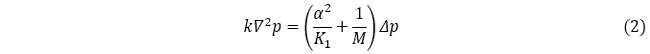
トンネル掘削後の地下水流れについて考えると、
トンネル掘削直後では間隙水圧分布に大きな変化はなく、その後、壁面からの湧水によって間隙水圧が減少していきながら、地盤の収縮変形が生じます。このとき、トンネル壁面以外の境界は変位が拘束されています。このような状況は、1次元圧密問題とよく似ています。
仮にトンネル掘削後の間隙水圧の変化が1次元圧密問題と同様の式で表されるとすると、第3回でも示しましたが、
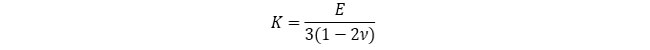
であることを考慮して、
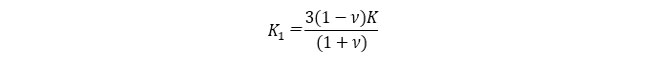
となります。今回の解析では、ν=0.2としていることから、となります。今回の解析では、
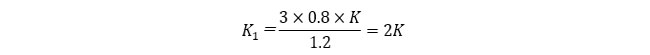
となり、圧密方程式は疑似連成解析の地下水流れの式に一致します。
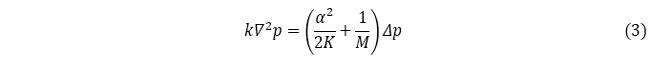
このことは、K1に現れる ![]() が境界条件の影響を表しており、ν=0.2の場合に、たまたま圧密方程式(2)が近似式(3)と一致することを示しています。圧密方程式は完全連成解析の支配方程式そのものであることから、ν=0.2の場合に完全連成解析の解と擬似連成解析の解とが一致することがわかります。
が境界条件の影響を表しており、ν=0.2の場合に、たまたま圧密方程式(2)が近似式(3)と一致することを示しています。圧密方程式は完全連成解析の支配方程式そのものであることから、ν=0.2の場合に完全連成解析の解と擬似連成解析の解とが一致することがわかります。
また、このことは、トンネル掘削後の地下水流れが1次元圧密問題と同様の式で表されることも示唆しています。
では、νが0.2以外の場合はどの程度の近似度が見込まれるのでしょうか。これを調べるため、ポアソン比を0.1と0.3とした場合について、同様の解析を行いました。
結果を以下に示します。結果を見ると、ポアソン比が0.1でも0.3でも擬似連成解析が完全連成解析をよく近似していることがわかります。
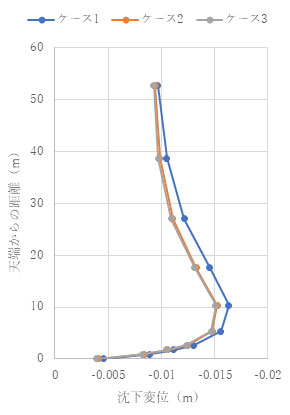
(ν= 0.1)t = 1.0e+4 (s)
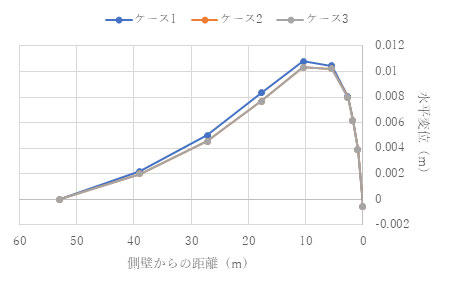
(ν= 0.1)t = 1.0e+4 (s)
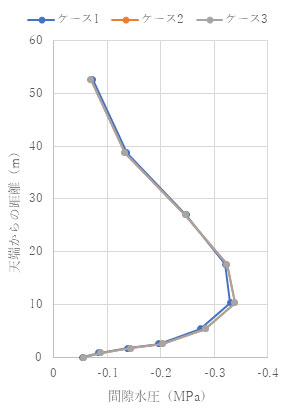
(ν= 0.1) t = 1.0e+4 (s)
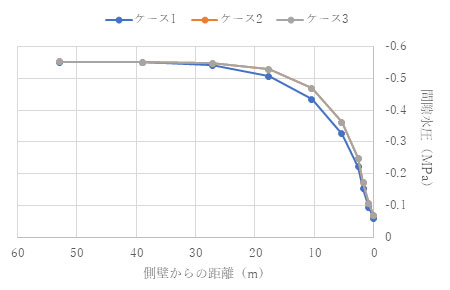
(ν= 0.1) t = 1.0e+4 (s)
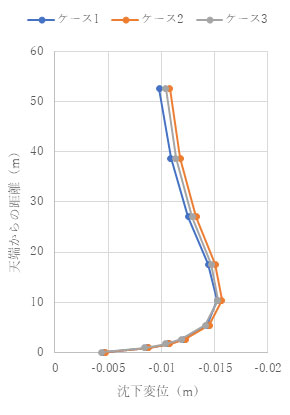
(ν= 0.3) t = 1.0e+4 (s)
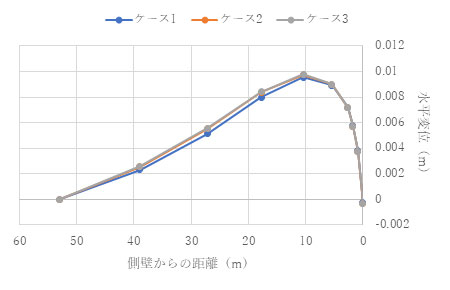
(ν= 0.3) t = 1.0e+4 (s)
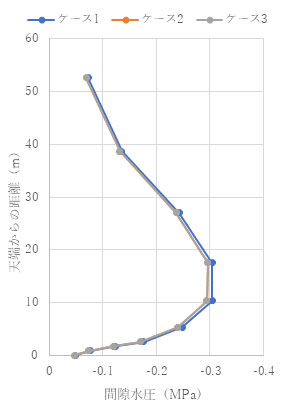
(ν= 0.3) t = 1.0e+4 (s)
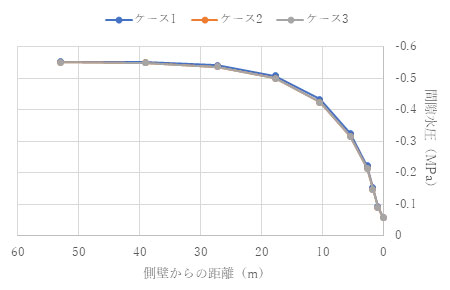
(ν= 0.3) t = 1.0e+4 (s)
これまで見てきたとおり、圧密問題とトンネル掘削の場合には、ポアソン比にもよりますが完全連成解析と擬似連成解析で、ほぼ一致した解が得られました。
計算時間は完全連成解析>擬似連成解析≫任意の時間解析となっています。特に、任意の時間解析では変形を求めるための計算が少なく、大幅な計算時間の短縮が望めます。
次回は、完全連成解析と擬似連成解析とで解が異なる場合の例を紹介します。

